Being able to quickly calculate in your mind the difference or sum of two or even three-digit numbers is an important skill that will not only help you quickly pass the test and impress the teacher, but also make math clearer and more interesting. In the article, I will talk about 6 interesting ways to learn how to count quickly and without a calculator.
In our circle, we often encounter the fact that children do not calculate well in their minds. In some programs, children in 2nd grade are taught to count in a column, and they begin to do all the calculations on paper. Or the guys learn the most popular way of counting “tens separately, units separately” and apply it in all cases.
For example, 45 + 19 is considered as 40 + 10 + 5 + 9 = 50 + 14 = 64. This is also possible, but it is not always convenient and fast. Instead, you can calculate 45 + 20 – 1 = 65 – 1 = 64.
We practice such cunning counting techniques at the circle in almost every lesson: after that, our students become more confident in school lessons and make fewer mistakes in their decisions. In this article, we will talk about tricks for addition and subtraction. You can practice them with your children: they work on different numbers, so it doesn’t matter if you have a child in 1st grade or 4th.
Table of Contents
Commutative and associative properties
These are the most basic tricks. They are studied at school, but we additionally train them: it is important for a child to learn to see numbers that are convenient for addition, and not to add everything in a row.
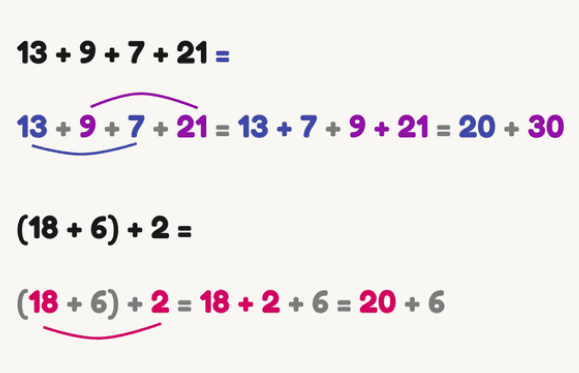
Adding an almost round number
Adding “round” numbers, that is, whole tens, hundreds, and so on, is always convenient. Therefore, if the term is close to round, it can be represented as the difference between this round number and the “extra” units:
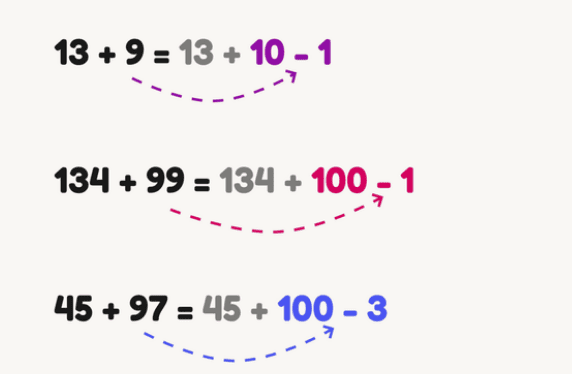
35 + 6 = 35 + 10 – 4 – you can do this too, but it’s not very convenient. The method works well with numbers ending in numbers greater than six: 7.8 and 9. Here and in other methods, it is important that the child already knows the composition of the number 10 well. And he understands how much to add to the number so that the sum becomes ten.
Subtraction of an almost round number
Here the idea is the same as in the previous trick: it is more convenient to subtract a round number, so we can represent the subtrahend as the difference between a round number and “extra” units:
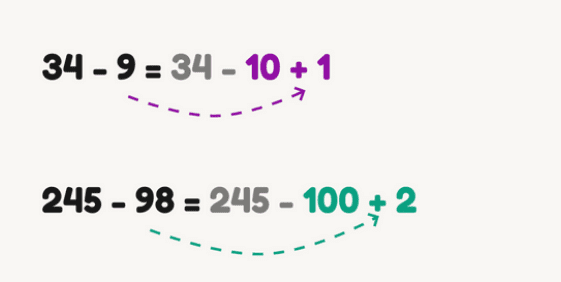
Be careful when practicing this technique: children sometimes make mistakes in it and apply it like this: 45 – 18 = 45 – 20 – 2 = x, but it should be: 45 – 18 = 45 – 20 + 2 = x. To avoid mistakes, pronounce the actions: we had to subtract 18, but we take 20 from 45, which is 2 more units. This means that we must “return” the deuce, that is, add 2.
Decomposition into convenient terms (addition)
The essence of the technique is that we break an example from one action into two actions that are easy to perform. This method is difficult for children at first, but after mastering it in practice, it helps a lot with counting.
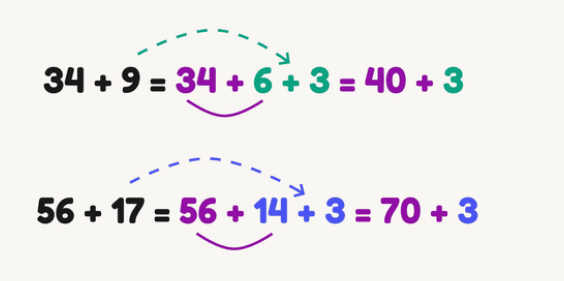
Decomposition into convenient terms (subtraction)
Here we apply the same idea as in the previous trick – we are looking for how to decompose the number that we subtract, so that it is more convenient to calculate.
This technique is well suited if the units of the minuend are less than those of the subtrahend.
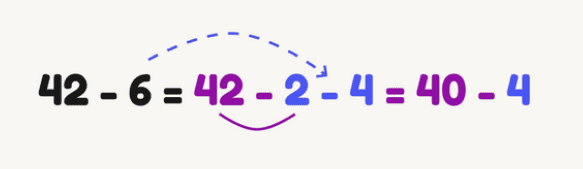
Subtraction with addition
This method is unusual and difficult to understand at first, but after mastering it, it makes it easy to subtract even large numbers without a calculator.
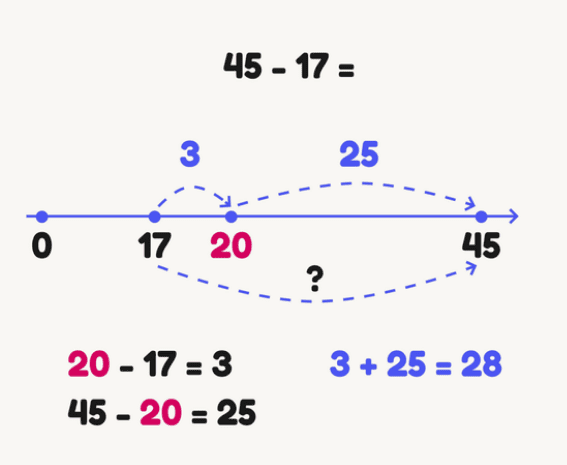
Let’s look at an example: 45 – 17 =
The first thing to understand is that subtraction is finding the distance between the numbers 17 and 45 on the number line.
Let’s choose on a straight line a round number between 17 and 45, to which it is more convenient for us to calculate the distance. Let it be 20.
17 to 20 distance 3
from 20 to 45 distance 25
So the total distance is: 25 + 3 = 28
Shall we practice? Even such a “terrible” example can be easily calculated using this method: 317 – 129 =
Between 371 and 129 we choose a round number – 200.
from 129 to 200 distance 71.
from 200 to 317 distance 117.
117 + 71 = 188.
We could choose 300 as the number “in the middle”. What kind of intervals to consider is not so important, the main thing is that it is convenient to calculate.
Understanding these techniques helps automate mental counting. It is not at all necessary to apply them all later – everyone chooses for himself what is more convenient and better remembered.

