HCF means Highest Common Factor. Now, What is the factor?
A factor is a number that divides the given number completely eg: 2 divides 4 completely therefore 2 is a factor of 4.
To find HCF of given numbers.
Firstly, we find factors of given numbers.
In the 2nd step, we write common factors of given numbers.
And in the final step, we write the Highest Common factor (HCF)
Note: The greatest number that divides the numbers completely is called HCF of the numbers.
Methods of HCF
HCF by Factorisation method
Let us take a example:-
Example 1: Find the HCF of 18 and 36
Factors of 18 = 1,2,3,6,9,18
Factors of 36 = 1,2,3,4,6,9,12,18,36
Common Factors of 18 and 36 = 1,2,3,6,9,18.
Highest Common factor (HCF) = 18.
Since 18 is the highest number that divides both the numbers 18 and 36 completely.
HCF by Prime Factorisation Method
We take the same example as above:
Prime factors of 18 = 2 x 3 x 3
Prime factors of 36 = 2 x 2 x 3 x 3
Common factors = 2 x 3 x 3
Now, Product of common factors = HCF
∴ HCF = 18
HCF by long division method
Let us take an example:
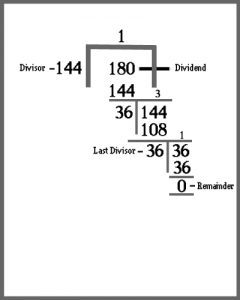
Find HCF of 144 & 180 by long division method.
Steps:
- Divide the larger number by the smaller number.
- After division, we get quotient and remainder
- Now in the next step, the remainder becomes the new divisor & the original divisor becomes the new dividend.
- Repeat the above step again and continue the process till you get zero as a remainder.
- The last divisor in the process is the HCF of the numbers.
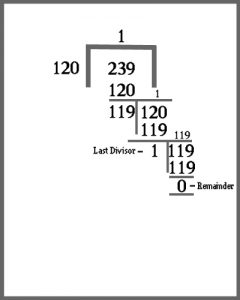
Let us take another example:
Find HCF of 120 & 239
So, HCF of 120 and 239 = 1
Remember:
1. HCF of two consecutive numbers is always 1.
e.g: HCF of 4 & 5 = 1, 9& 10 = 1 etc.
2. HCF of two consecutive even numbers is always 2.
e.g: HCF of 2 & 4 = 2 and HCF of 20 & 22 = 2 etc.
3. HCF of two consecutive odd numbers is always 1.
e.g: HCF of 11 and 13 = 1, HCF of 25 and 27 = 1 etc.
LCM (Lowest Common Multiple)
Lowest Common Multiple (LCM) of the two or more numbers is the smallest number that is completely divisible by the numbers.
Example: Find LCM of 3 and 6?
Multiples of 3 = 3,6,9,12,15,18,21,24,27,30…
Multiples of 6 = 6,12,18,24,30,36,42,48…
Common multiples = 6,12,18,24,30…
Now 6 is the lowest common multiple
Lowest common multiple = 6.
LCM by prime factorisation method
Example: Find LCM of 6,8 and 12.
Prime factors of 6 = 2 x 3
Prime factors of 8 = 2 x 2 x 2
Prime factors of 12 = 2 x 2 x 3
= 2 x 2 x 3 x 2
= 12 x 2 = 24
= LCM of 6, 8 & 12 = 24
Note: Multiply the common factors & the factors left out.
LCM by Long division method
Example:
Find LCM of 60, 70, 108.
| 2 | 60 | 70 | 108 |
| 2 | 30 | 35 | 54 |
| 3 | 15 | 35 | 27 |
| 3 | 5 | 35 | 9 |
| 3 | 5 | 35 | 3 |
| 5 | 5 | 35 | 1 |
| 7 | 1 | 7 | 1 |
| 1 | 1 | 1 |
= 2 x 2 x 3 x 3 x 3 x 5 x 7
= 12 x 9 x 5 x 7
= 108 x 5 x 7
= 540 x 7
= 3780
So, LCM of 60, 70, 108 = 3780
Relationship between HCF and LCM
| Numbers | HCF | LCM | Product of Numbers | Product of HCF & LCM |
| 6, 8 | 2 | 24 | 6 x 8 = 48 | 2 x 24 = 48 |
| 15, 30 | 15 | 30 | 15 x 30 = 450 | 15 x 30 = 450 |
| 40, 50 | 10 | 200 | 40 x 50 = 2000 | 10 x 200 = 2000 |
From the above table we conclude that the product of the numbers always equal to the product of their LCM & HCF.
Product of the number = LCM x HCF.
LCM = Product of two numbers ÷ HCF
HCF = Product of two numbers ÷ LCM