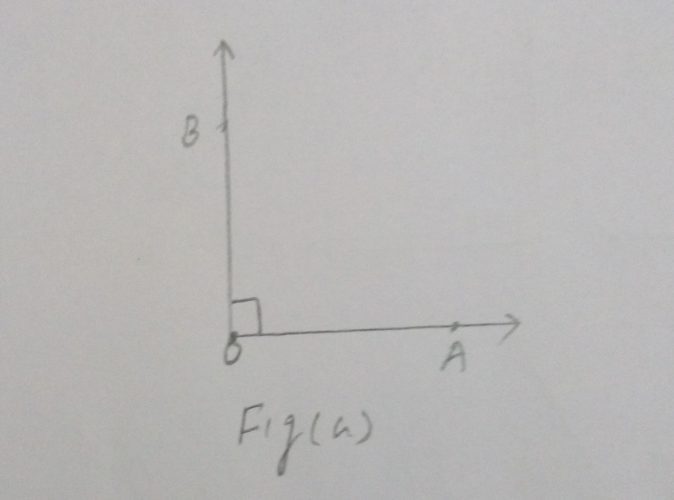
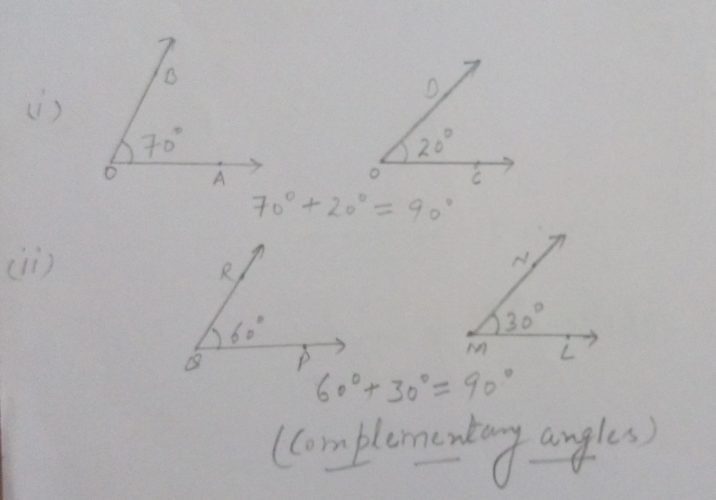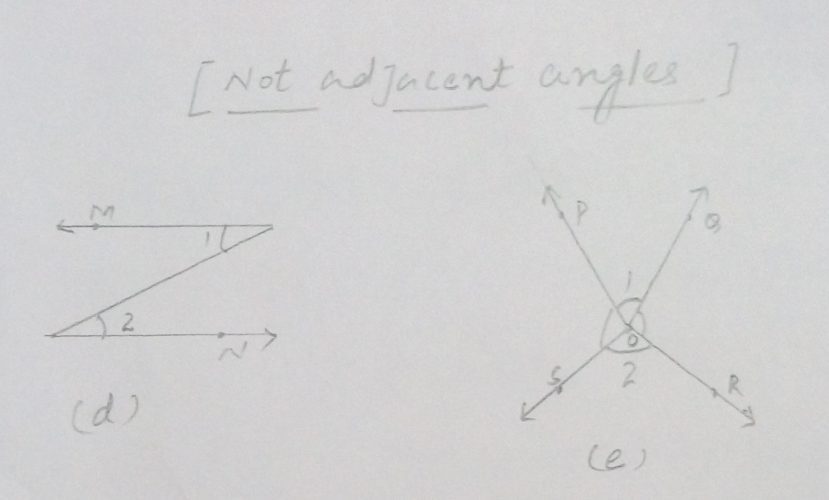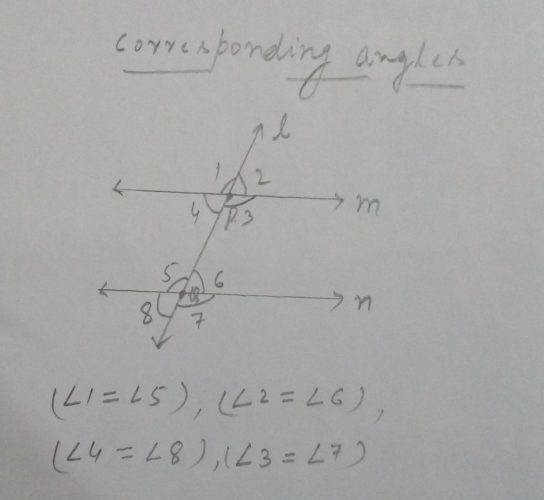An angle is made up of two rays with a common end point called a vertex. The two rays of the angle are also called arms of the angle.
If fig (a) OA and OB are two rays and O is Vertex.
There are different types of angles such as acute angle, right angle, obtuse angle, straight angle, and reflex angle.
Now, we discussed some more types of angles.
Complementary angles:
Two angles whose sum is 90 degrees are called complementary angles.
Here are some examples of complementary angles.
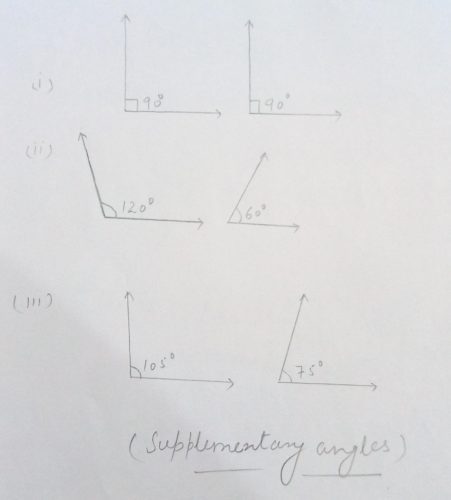
Supplementary angles. Two angles whose sum is 180 degrees are called supplementary angles.
Here are some examples of supplementary angles.
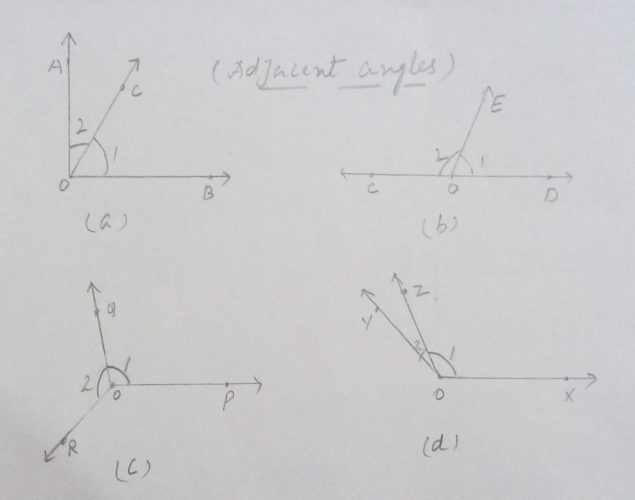
Adjacent angles. Two angles are said to be adjacent if they have a common vertex and a common arm between the remaining two uncommon arms are called adjacent angles.
Some examples of adjacent angles are:
In Fig (a) angle 1 and angle 2 are adjacent angles, because they have a common vertex ‘O’ and a common arm (OC) between two uncommon arms (OA & OB)
In Fig (b), (c), (d) ∠1 and ∠2 are also adjacent angles.
In Fig (d) ∠1 and ∠2 are not adjacent angles because they do not have a common vertex and in fig (e) ∠1 and ∠2 are also not adjacent angles because they do not have a common arm.
Note:
- Two adjacent angles can be complementary angles {See Fig (a)}
- Two adjacent angles can be supplementary angles. {See Fig (b)}
- Two obtuse angles can be adjacent angles {See Fig (c)}
- An acute angle can be adjacent to an obtuse angle. {See Fig (d)}
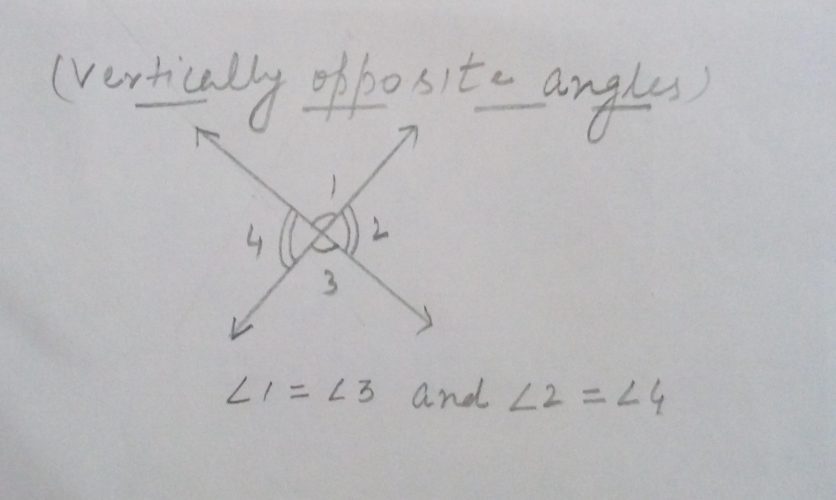
Vertically Opposite Angle. Vertically opposite angles formed when two lines (Say AB and CD) intersect each other at the point (Say O) (See Fig)
There are two pairs of vertically opposite angles.
In given fig. ∠1 and ∠3 are vertically opposite angles and ∠2 and ∠4 are also vertically opposite angles.
Note: Vertically opposite angles are always equal.
Corresponding Angles. A line that intersects two or more lines at distinct points is called a Transversal (See Fig)
Line l intersects line m and n at points P and Q respectively. Therefore line l is a transversal line.
In the given fig. eight angles are formed.
The pairs of corresponding angles are (∠1, ∠5), (∠2, ∠6), (∠4, ∠8), (∠3, ∠7)
Corresponding angles are always equal.